<<  | 1 | 2 | 3 | 4 |  >>

К разделам «Статика» и «Динамика» дано введение, в котором изложены аксиомы динамики и статики. Отметим, что Жуковский вводит теорему параллелограмма сил (а не аксиому) и доказывает ее на основании положений динамики. Кроме того, аксиому он доказывает, основываясь на законе инерции, кинематических формулах и понятии девиации.

Статика занимает большой объем курса, включает теорию приведения и равновесия сходящихся и параллельных сил, много места уделено определению центров тяжестей конкретных тел, изложена теория моментов силы, доказана теорема: «Пара не имеет равнодействующей», изложена теория пар сил, доказана основная теорема статики.

В главе «О равновесии» доказаны условия равновесия различных систем сил, приведены примеры равновесия тел под действием плоской и пространственной систем сил.

Завершается курс теоретической механики разделом «Динамика точки». Выводятся уравнения движения точки в инерциальной системе отсчета, рассматриваются различные виды дифференциальных уравнений для свободной точки и методы их интегрирования. Решаются задачи о прямолинейном и криволинейном движениях точки, многие эти задачи вошли сейчас в известные задачники.

Выводятся общие теоремы динамики для материальной точки, рассматривается движение точки под действием центральной силы, рассматривается теория потенциального поля, большое место уделено задачам о движении планет.

Завершается раздел главой о равновесии и движении несвободной материальной точки. Выводятся дифференциальные уравнения движения точки по гладкой поверхности и линии. Определяется давление точки на опору, решены задачи о движении математического маятника. Выводятся дифференциальные уравнения относительного движения материальной точки, решается ряд задач на эту тему.

Курс «Аналитическая механика» Николай Егорович читал в МВТУ с 1874 по 1920 гг. (свыше 40 лет). Этот курс видоизменялся и совершенствовался на протяжении времени, учитывая потребности практики (техники). Основное содержание курса сложилось к концу 19-го века и все издания после 1902 г. перепечатывались с небольшими дополнениями, которые вносил Жуковский в связи с развитием техники.

Курс содержит разделы – кинематика точки и системы, динамика и статика свободной и несвободной точки, динамика и статика механической системы, ньютоновский удар, применение метода Лагранжа к задачам на упругие системы.

Раздел «Кинематика точки» изложен компактно, содержит четкое разбиение по параграфам, в которых излагаются способы задания движения точки; все положения четко доказаны. Кинематика системы включает формулы Эйлера для проекций скорости точки твердого тела, вращающегося около неподвижной точки на прямоугольные оси координат, имеющие начало в этой же неподвижной точке; формулы для «скорости точки свободного твердого тела»; «теорему Кориолиса и аналитическое выражение проекций поворотного ускорения». Здесь же содержится правило для построения поворотного ускорения (правило Жуковского). Отметим, что Жуковский определял направление вектора угловой скорости так, чтобы наблюдатель, из конца вектора в его начало, видел вращение тела совершающимся по часовой стрелке (а не против часовой стрелки).

Раздел «Динамика точки» построен во многом так же, как и в Лекциях, вып. 5, но в «Аналитической механике» более четкое разбиение раздела на подразделы (движение планет, равновесие несвободной материальной точки, движение несвободной материальной точки, об относительном движении материальной точки), а также даны примеры их технического приложения.

Излагая «Статику системы», Жуковский вводит определение механической системы, определение связи, проводит классификацию связей и вводит понятие числа степеней свободы механической системы, дает определение возможного перемещения точки, очень подробно излагает доказательство принципа Лагранжа (о равновесии системы) методом Ампера, добиваясь доказательства принципа «во всей полноте», рассматривает равновесие гибкой нити.

«Динамика системы» начинается с «принципа Даламбера» и общего уравнения динамики, здесь же излагается запись общего уравнения динамики в обобщенных координатах и условия равновесия (или движения) в обобщенных координатах (дифференциальные уравнения движения).

Общие теоремы динамики выводятся из общего уравнения динамики системы.

«Теорема о движении центра тяжести» (центра масс) изложена с различными частными случаями, подробно описано действие прибора Теплера, наглядно показывающего, что «внутренние силы, вызывающие относительное перемещение частей системы, не могут привести в движение ее центр тяжести или изменить его движение».

Теорема об изменении кинетического момента системы и законы сохранения кинетического момента также проиллюстрированы глубокими примерами. Разобрана теория движения человека на вращающейся скамье при наличии начальной угловой скорости системы человек-скамья (w₀) . Естественно, что с увеличением момента инерции системы человек-скамья относительно оси вращения (руки человека разведены в стороны) J_z , угловая скорость системы уменьшается

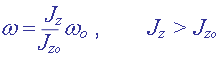
Указано на ошибку Delaynay, объясняется, что если нет начальной угловой скорости системы человек-скамья, то по теореме площадей имеем

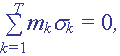
где  m_k, s_k  –  масса и площадь, ометаемая радиусом-вектором k-той точки.

Жуковский объяснил, что если человек рукой ометает некоторую площадь в плоскости, перпендикулярной оси вращения, то скамья с человеком вокруг своей оси повернется на некоторый угол в сторону, противоположную движению руки.

Теорема об изменении кинетической энергии доказана в дифференциальной и интегральной формах, введено понятие потенциальной энергии и получен закон сохранения механической энергии.

Геометрия масс, теория главных осей инерции тела, динамическое уравновешивание вращающегося тела изложены полно, выведены динамические уравнения вращательного и плоскопараллельного движения твердого тела.

Решены задачи о движении физического маятника вокруг неподвижной и совершающей возвратно-поступательное движение горизонтальной оси. Первая иллюстрирует использование уравнения вращательного движения, вторая посвящена теории вынужденных колебаний системы с кинематическим (инерционным) возбуждением. Даны другие примеры применения уравнений динамики системы к решению задач.

Добавление приложения метода Лагранжа к задачам строительной механики было сделано в 1910 году. Здесь даются «приемы решения задач на неопределенно- статические системы, исследование которых часто затрудняет конструкторов».

Курс «Теория регулирования хода машин» Н.Е. Жуковский прочел в 1908-1909 учебном году студентам МВТУ. Появился в печати в 1909 г. Этот курс является очень хорошим приложением теоретической механики к практическим задачам. В этой книге разобрано применение уравнений Лагранжа 2-го рода, рассматриваются малые колебания механической системы, проведены аналитические и численные исследования решений. Книга имеет высокий физический и математический уровень.

Курс лекций «Прикладная механика» читался Жуковским в Московской практической академии коммерческих наук и был издан в 1901 г. литографическим путем студентом МВТУ В.И Владимировым «Практическая механика есть наука о машинах». Курс включает в себя теорию механизмов, раздел о механике машин, теорию расчета динамики их, регулирование хода машин, излагается простейшая теория гидравлических, воздуходувных машин.

Здесь не касаемся других читаемых Н.Е. Жуковским курсов. Рассмотренные выше учебные курсы настолько полны и хорошо написаны, что вполне составляют конкуренцию современным курсам по механике с точки зрения объема излагаемого материала, качества изложения, разносторонности подготовки и высокой научной квалификации автора.

В предисловии редакции (ГИОП, М-Л., 1939 г. Полн.собр.соч.) отмечается: «И надо полагать, что слава, которую снискало МВТУ в ряду других русских втузов, главным образом, обязана тому, что механику в нем преподавал Н.Е. Жуковский».

Николай Егорович сопровождал свои лекции и практические занятия иллюстрациями положений механики на специальных приборах, иллюстрировал задачи моделями механизмов, старался привить выпускникам МВТУ инженерные навыки. Им и его учениками была создана коллекция приборов Жуковского на кафедре «Теоретическая механика».

Во многих разделах своих классических курсов он находил новые подходы к изложению материала, свои механические трактовки теорем, следствий из теорем, критически анализировал научные материалы других ученых, приводил практические примеры.

Научные работы Н.Е. Жуковского по теоретической и аналитической механике внесли существенный вклад в развитие механики и являлись источником развития читаемых им лекционных курсов.

Жуковским написано 68 работ по теоретической и прикладной механике (включая работы по астрономии и прикладной математике). Здесь отметим некоторые работы Жуковского по теоретической и аналитической механике.

Ряд ранних работ посвящен соударению тел («О соударении тел» 1871 г., «К вопросу о наибольшем ударе» 1880 и др.). В курсах «Теоретическая механика», «Аналитическая механика» неизменно присутствуют разделы по теории ньютоновского удара. В этих разделах рассматриваются общие теоремы динамики при ударе, вопросы о центре удара, об ударе двух шаров, о косом ударе, теорема Карно, а также об определении коэффициента восстановления.

В курс аналитической механики Н.Е. Жуковского включен раздел о равновесии гибкой нити.

Есть у него и весьма интересная исследовательская статья «Связь между вопросами о движении материальной точки и о равновесии гибкой нити» (1879 г.).

Н.Е. Жуковский провозгласил идею добротного политехнического образования, в котором главное – сочетание высокого уровня теоретической подготовки с привитием навыков решения практических задач и с анализом геометрии движения, наглядностью и простотой представления движения механических систем.

Этой идее посвящена его статья «О значении геометрического истолкования в теоретической механике» (Матем.сборн., 1896, т. 18, вып. 1). В этом же году он опубликовал статью «Геометрическая интерпретация рассмотренного С.В. Ковалевской случая движения тяжелого твердого тела около неподвижной точки». В ней проведен тщательный анализ общих свойств движения тела с одной неподвижной точкой в случае, который был открыт Ковалевской в 1888 году. Сейчас уже этот классический материал вошел в учебники. В 1888 г. Н.Е. Жуковский написал работу «Элементарная теория гироскопов». В настоящее время объяснение правила вынужденной прецессии входит в учебники теоретической механики как правило прецессии Жуковского.

В России 18 и 19-го веков сложилась школа механики – школа Остроградского, основным принципом которой является сознательное сочетание теории с практикой. Преподавание механики Жуковским в Московском университете также было подчинено этому принципу. В статье «Механика в Московском университете за последнее пятидесятилетие» (1911 г.), характеризуя труды Н.Д. Брашмана, Ф.А. Слудского, свои и С.А. Чаплыгина, писал: «Мне кажется, что этот девиз – решение определенных реальных задач механики – явился руководящим для большинства учеников московской школы теоретической механики».

Николай Егорович глубоко понимал механику, ее основы, изучал труды классиков механики, труды других ученых механиков. Немало работ Жуковского посвящено глубокому анализу научных трудов ряда ученых.

Н.Е. Жуковским написаны статьи: «Ньютон как основатель теоретической механики» (В кн. Двухсотлетие памяти Ньютона (1687-1887). М., 1888, с. 13-20, «О трудах С.В. Ковалевской по прикладной математике». Матем.сб., 1891, т. 16, вып. 1, с. 10-20).

Николай Егорович в статье «Ученые труды М.В. Остроградского по механике» (Матем.сб., 1902, т. 22, с. 533-573) сделал обзор работ основателя школы русской механики.

Позднее им была написана статья «О работах В.Я Цингера по механике» (Матем.сб., 1911, т. 28, вып. 1, с. 50-53).

Все эти работы говорят о том, как глубоко вникал Жуковский в суть задачи механики, как хорошо был знаком с работами классиков механики и крупных механиков.

Научные работы Николая Егоровича питали его педагогическую деятельность, позволяли во всех тонкостях разбирать основные положения механики и рассматривать ее приложение к конкретным практическим задачам. Такое исключительное сочетание научной, учебной и практической деятельности привлекало множество студентов, которые постоянно обращались к Жуковскому за практическим советом и работали с ним и после окончания училища.

<<  | 1 | 2 | 3 | 4 |  >>