<<  | 1 | 2 | 3 | 4 |  >>

Своей любовью к образному, геометрическому мышлению В.Я. Цингер увлекал молодых механиков, направляя их труды по тому пути, по которому следовали великие геометры Ньютон, Пуансо, Понселе и Шаль». (Материалы музея Н.Е. Жуковского).

Позднее Н.Е. Жуковский вспоминал: «Мне приятно теперь отметить мои совместные работы с профессорами московского университета, в число которых я имел честь вступить в 1887 г. Ф.А. Бредихин охотно вводил меня в различные интересующие его в то время вопросы … Во время моего пребывания в университете лекции по механике параллельно вели Ф.А. Слудский и В.Я. Цингер. Я с благодарностью вспоминаю теперь двух моих учителей, из которых один разъяснил нам широкое значение общих аналитических метод, а другой указал силу геометрических толкований рассматриваемых явлений». (Из речи Н.Е. Жуковского на торжественном заседании по поводу 40-летия его ученой деятельности. 15.01.1911).

Эти два подхода к исследованию задач механики Н.Е. Жуковский оценивал так: «Отстаивая достоинства геометрического метода исследования, я далек от мысли об его исключительности. Механика должна равноправно опираться на анализ и геометрию, заимствуя от них то, что наиболее подходит к существу задачи … Анализ дает нам могущественное оружие для разрешения задач динамики. Но последняя обработка решений задачи всегда будет принадлежать геометрии». (Материалы музея Н.Е. Жуковского).

Можно сказать, что Жуковский произвел революцию в построении и изложении курса механики высшей школы. Вместо изложения теоретической механики в стиле аналитической механики Лагранжа он вводит в механику геометрический метод. Он писал, что «если могут быть споры о самостоятельной роли геометрии при решении недоступных до сих пор задач динамики, то ее высокое значение в преподавании не подлежит сомнению. Ум изучающих весьма часто склонен к формальному изложению. Я из своего педагогического опыта знаю, как часто запоминаются формулы без усвоения стоящих за ними образов. Как это не кажется странным, но одним из затрудняющих вопросов является иногда вопрос о значении той или иной буквы в бойко написанной формуле. В этом отношении геометрическое толкование, предпочтение геометрического толкования аналитическому всегда приносит пользу. Если формулы и подстановки некоторыми из учащихся легко запоминаются, то также скоро исчезают бесследно из памяти, но раз усвоенные геометрические образы, рисующие картину рассматриваемого явления, надолго западают в головы и живут в воображении учащегося». (полн. собр. соч., М., 1937, т.IX, с. 185).

Н.Е. Жуковский подчеркивал в своих лекциях и выступлениях на научных съездах, что «механика развивалась как глубокомысленными трудами аналитиков, так и остроумными исследованиями геометров. При этом часто бывало, что сложные аналитические формулы освещались и представлялись в ясной наглядной форме благодаря удачным геометрическим представлениям. Такие интерпретации охватывали задачу во всей ее полноте и раскрывали многие свойства ее, не замеченные при аналитическом исследовании. Так было с решением задачи о движении твердого тела около его центра тяжести: решение сперва было получено Л. Эйлером аналитическим путем, но оставалось затерянным среди массы формул и только благодаря простым и наглядным интерпретациям Л. Пуансо предстало перед глазами ученых со всей ясностью». (Н.Е. Жуковский. Полн. собр. соч., М., 1937, т. IX, с. 313).

Подчеркивая большое значение геометрических методов исследования в механике, Н.Е. Жуковский говорил о «чувстве меры». Он писал: «Говоря о высоком значении геометрического толкования для преподавания теоретической механики, не скрою, что некоторые авторы геометрией злоупотребляют. Нагромождение кинематических теорем, так же как и нагромождение формул, только запутывает дело преподавания. Геометрическое толкование должно быть ясно и просто и должно всегда близко прилегать к рассматриваемой задаче». (Н.Е. Жуковский. Полн.собр.соч., 1937, М., т. IX, с. 185, 186).

Н.Е. Жуковский считал целесообразным в преподавании широкое развитие лекций. Общеизвестно его высказывание, что по силе впечатления лекционный способ стоит выше других приемов преподавания и ничем не заменим, вместе с тем этот способ есть и самый экономный во времени.

 Кроме того, последовательно изложенный курс лекций дает не только фактический материал, который будет спрашиваться на экзаменах, а нечто гораздо более важное – основы современного научного мышления. Если же на процесс высшего образования смотреть как на совокупность подлежащих сдаче экзаменов, то, очевидно, самостоятельная работа студента по учебнику с некоторой помощью «консультантов-репетиторов» полностью решает дело. Однако весь опыт развития высшей школы и в нашей стране, и за рубежом свидетельствует, что слушание лекций выдающихся профессоров имеет какое-то особо ценное значение, представляет важнейший процесс приобщения к творческой деятельности ученого. В лекциях перед слушателями раскрывается как бы лаборатория научного мышления, показывается историческое становления научной истины, выявляются качество мышления лектора и его воззрения на идеалы науки и цель научного мышления. Только на лекциях можно понять сущность той или иной научной школы. Только на лекциях можно услышать оценки новых научных методов исследования и ясно понять, что внес в сокровищницу мировой научной мысли сам лектор, насколько близок ему и плодотворен процесс созидания новых интеллектуальных ценностей. К такому идеалу лекционного преподавания был очень близок Н.Е. Жуковский.

Б.И. Россинский, один из его учеников, позднее писал, что несмотря на отсутствие ораторского искусства и высокий, почти дискантный голос лектора, вся аудитория с напряженным вниманием жадно ловила каждое его слово. Этого Николай Егорович достигал умелой постановкой вопроса, логичностью его изложения, своей исключительной эрудицией. Разрешая один вопрос, он выдвигал новый, заинтересовывал молодежь кажущейся неразрешимостью его. Но знание и логика были на стороне ученого, и как светлели лица студентов, когда мелок Николая Егоровича решал на доске казавшееся неразрешимым. (Воспоминания Б.И. Россинского. Из материалов музея Н.Е. Жуковского).

По понедельникам, четвергам и субботам Н.Е. Жуковский читал лекции в Техническом училище. Курс теоретической механики он разделил на 2 части: первый год читалась так называемая теоретическая механика в составе геометрической статики, геометрической кинематики и начал динамики в элементарном изложении; на втором году читалась аналитическая механика, куда входила аналитическая часть кинематики и полный курс динамики точки и твердого тела вместе с аналитической статикой.

По средам и пятницам – в Московском университете читал механику точки, теорию притяжения, гидромеханику, руководил упражнениями (по 6 часов в день).

Один раз в неделю читал 2-х часовую лекцию в Коммерческой академии на Покровском бульваре.

Курсы, читаемые Н.Е. Жуковским в Техническом училище:

Н.Е. Жуковский выработал прекрасное, ставшее классическим изложение основ теоретической механики, которое было издано в литографированном виде. К этой работе широко привлекались студенты. Так, например, «Аналитическая механика. Лекции проф. Н.Е. Жуковского и Приложение чертежей к Аналитической механике» проф. Н.Е. Жуковского (издано отдельной книжкой) были подготовлены студентом Ф.Ф. Бартом.

Студент В.П. Ветчинкин стенографировал, обработал и издал курс лекций проф. Н.Е. Жуковского по теоретическим основам воздухоплавания. «Прикладная механика». Курс лекций проф. Н.Е. Жуковского (Московская практическая академия коммерческих наук) издал студент В.Н. Владимиров. Лекции по гидродинамике – единственный курс, который был Н.Е. Жуковским напечатан в обработанном виде.

Вот что писал об том курсе академик Л.С. Лейбензон: его курс механики был настолько прост и понятен студентам, что получил распространение по всей России. И только изучив по литографическим запискам курс Н.Е. Жуковского, студенты приступали к изучению трудных курсов своих профессоров. Кафедра теоретической механики Императорского Московского технического училища во главе с Н.Е. Жуковским сделалась всероссийской кафедрой механики. (Лейбензон Л.С. Н.Е. Жуковский (К 100-летию со дня рождения). М-Л., 1947).

После 1905 г. в преподавании механики были проведены реформы и были введены обязательные упражнения по механике, постановкой которых руководил Н.Е. Жуковский. Он сам составлял задачи для этих упражнений, и они велись под его непосредственным руководством.

Жуковский большое внимание уделял частным задачам механики. Академик Л.С. Лейбензон писал, что Н.Е. Жуковский старался выбирать такие задачи, чтобы математический анализ был по возможности прост, и на первый план выступала механическая суть. Задачи, не интересные математически, но важные для техников, представлены очень полно. Разделяя известное высказывание И. Ньютона о том, что «в механике примеры учат не меньше, чем правило», Жуковский вел ежегодно практические занятия со студентами и сам принимал зачеты, требуя, чтобы в специальных тетрадях были представлены подробные решения методически тщательно подобранных задач. (Лейбензон Л.С. Н.Е. Жуковский. М-Л., 1947).

Н.Е. Жуковский считал, что лектор должен руководить практическими занятиями по механике, чтобы иметь возможность проверять усвоение студентами предмета и обеспечить руководство на начальных стадиях обучения.

Н.Е. Жуковский наряду с профессором И.В. Мещерским был одним из пионеров, применившим теоретическую механику к практическим вопросам техники.

Жуковский составлял задачи на специальных карточках, где была сформулирована задача, и был дан ответ.

В Техническом училище были изданы литографическим способом под именем Н.Е. Жуковского и, несомненно, в какой-то степени им авторизованные студенческие издания сборника задач (например, издания 1891, 1907 гг.) и посмертное издание 1922 г., вышедшее под редакцией В.П. Ветчинкина. В этом издании к материалу студенческих изданий, вышедших ранее, добавлены задачи с карточек Н.Е. Жуковского и, кроме того, ряд дополнительных задач, относительно которых В.П. Ветчинкин писал в предисловии, что «о многих из этих задач я разговаривал лично с Николаем Егоровичем, причем он одобрил их к изданию в будущем своем сборнике».

Б.С. Зернов заменял Н.Е. Жуковского во время болезни. Зернову принадлежат три выпущенные в МВТУ очень ценных задачника по теоретической механике с решениями. Из них особенно важен задачник по кинематике, в котором он, как ассистент Н.Е. Жуковского, собрал очень большое число задач Жуковского на плоское движение, решаемых геометрическими методами.

Перечисленные выше курсы по теоретической, аналитической и прикладной механике неоднократно переиздавались учениками Николая Егоровича.

В полное собрание сочинений Жуковского (Гос.изд.оборон.промышл., М-Л., 1939), изданное под редакцией В.П. Ветчинкина и А.П. Котельникова вошли – лекции, выпуск 4:

Аналитическая механика. Теория регулирования хода машин. Прикладная механика.

Курс лекций (выпуск 5) Н.Е. Жуковский читал в Московском университете с 1886 по 1919 годы:

Кинематика. Статика. Динамика точки (ред. А.П. Котельников).

Лекции по кинематике включают разделы – кинематика точки, сложное движение точки; кинематика неизменяемой системы, сложение движений системы.

В «Кинематике точки» изучается движение точки в естественных осях, в прямоугольных декартовых координатах, в полярных координатах на плоскости, выводятся формулы для проекций скорости и ускорения точки на соответствующие оси, вводятся векторы скорости и ускорения точки.

Для каждого раздела даны подробные примеры.

В примере "даны уравнения движения в смешанных координатах  y = at,  j = bt "

Здесь y, j – декартова и полярная координаты точки; a, b – постоянные; t – время.

Далее определяется уравнение траектории в полярных координатах

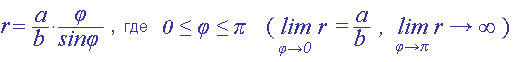
и строится кривая – траектория точки.

Получив зависимость r = r(j), Жуковский доказал возможность и единственность такого задания движения точки.

Теоремы сложения скоростей и ускорений выведены геометрическим методом. Особое внимание Жуковский уделяет вопросу построения Кориолисова (поворотного) ускорения, он излагает способ построения вектора поворотного ускорения, называемый сейчас «правилом Жуковского», которое вошло в современные учебники по теоретической механике.

Кинематика неизменяемой системы включает кинематику простейших движений системы – поступательного и вращательного, кинематику плоскопараллельного, сферического движений, а также общего случая движения системы.

Большое внимание уделено геометрии этих движений. Скорости и ускорения точек в последних двух движениях не рассматриваются.

В разделе «Сложение движений системы» рассматриваются сложение поступательных движений, вращательных движений вокруг пересекающихся и параллельных осей, сложение поступательных и вращательных движений. Все доказательства хорошо иллюстрированы чертежами.

В главе «Аналитическое исследование движений неизменяемой системы» Жуковский получает формулы Эйлера для проекции скорости точки системы при сферическом движении, а также скорости точки неизменяемой системы в общем случае движения путем дифференцирования координатных уравнений. Аналогично, дифференцированием выражений для проекции скорости точки получаются проекции ускорений точки неизменяемой системы (твердого тела) при сферическом движении и в общем случае движения.

Векторные соотношения для ускорения получены как следствия из уравнений проекций ускорений на оси координат.

Здесь же аналитически (с помощью дифференцирования) получены векторные формулы сложения скоростей и ускорений при сложном движении точки. Следует отметить актуальность полученных кинематических соотношений в связи с необходимостью использования ЭВМ для расчетов.

<<  | 1 | 2 | 3 | 4 |  >>