• Курс теории марковских процессов. Обозрение прикладной и промышленной математики. Серия "Вероятность и статистика", 2001, т. 8, вып. 1, с. 198-200. (Второй Всероссийский симпозиум по прикладной и промышленной математике. Тезисы докладов. Самара, 1 - 6 июля 2001 г.)

В Московском государственном техническом университете им. Н.Э.Баумана с 1998/1999 учебного года читается обязательный семестровый курс "Дополнительные главы теории случайных процессов" для студентов специальности "Прикладная математика" факультета "Фундаментальные науки". В учебном курсе излагаются основы аналитического метода для случайных процессов с дискретными состояниями. Для решения уравнений Колмогорова для пеpеходных веpоятностей марковских процессов используются методы обыкновенных дифференциальных уравнений, уравнений в частных производных, интегральные преобразования. Даются примеры прикладных задач, возникших в различных областях естествознания и техники на основе теории случайных процессов. Программа курса включает следующие разделы.

Целочисленные случайные величины и их производящие функции. Факториальные моменты. Мультипликативное свойство. Экспоненциальные производящие функции. Многомерные производящие функции.

Переходные вероятности однородных марковских процессов со счетным множеством состояний N = {0,1,2,...}. Инфинитезимальные характеристики и их вероятностная интерпретация. Классификация состояний. Вывод первой и второй (линейных) систем дифференциальных уравнений Колмогорова для переходных вероятностей.

Процессы гибели и размножения, вложенная цепь Маркова для которых является случайным блужданием. Оператор обобщенного дифференцирования Гельфонда-Леонтьева. Свертка с помошью производящих функций первой и второй систем уравнений для переходных вероятностей. Асимптотическое поведение средних для процессов чистого размножения пуассоновского, степенного и линейного типов. Процессы квадратичного и полиномиального типов.

Ветвящийся процесс и его уравнения. Вывод свойства ветвления для переходных вероятностей. Вывод нелинейного дифференциального уравнения Колмогорова. Интерпретация ветвящегося процесса через частицы. Приложения в физике. Цепная ядерная реакция размножения нейтронов T ® kT. Докритические, критические, надкритические процессы и вероятностный смысл параметра критичности. Вычисление вероятности вырождения ветвящегося процесса, исходя из стационарного первого уравнения.

Структура множества марковских процессов при дискретном фазовом пространстве Nⁿ. Марковские процессы с взаимодействием. Второе уравнение для многомерной производящей функции переходных вероятностей. Конструктивное описание как процессов с взаимодействием частиц. Схема взаимодействий. Иммиграция частиц, финальные частицы. Ветвящиеся процессы с взаимодействием. Первое и второе уравнения для экспоненциальной производящей функции и производящей функции переходных вероятностей (уравнения в частных производных). Ветвящиеся процессы. Свойство ветвления и нелинейная система обыкновенных дифференциальных уравнений.

Приложения в формальной химической кинетике. Виды кинетических уравнений. Детерминированная и вероятностная модели мономолекулярной реакции T₁ ® T₂. Явное решение уравнений Колмогорова. Предельная теорема при большом начальном числе частиц. Бимолекулярная реакция T₁ + T₂ ® T₃ и закон действующих масс. Бимолекулярная реакция 2T ® T. Приложения в экологии. Детерминированная и вероятностная модели системы "хищник-жертва". Применение статистического моделирования. Стохастическая модель эпидемии. Пороговая предельная теорема для финальных вероятностей. Приложения в технике. Вычисление стационарного распределения для системы массового обслуживания 0 ® T, T ® 0.

Сведения из истории развития теории случайных процессов. Макроскопический и микроскопический, детерминистический и стохастический, непрерывный и дискретный подходы при построении математических моделей сложных систем. Перечисление основных схем взаимодействий, задача классификации схем. Проблема вывода третьего (нелинейного) уравнения для специальных классов марковских процессов.

Для более глубокого освоения специального курса студентами выполняется типовой расчет по решению уравнений Колмогорова для марковских процессов. Методические материалы по дисциплине отражены в учебном пособии [5]. Содержание представляемого курса определено в основном монографиями и работами [1], [2], [3], [4], [6].

1. Гихман И.И., Скороход А.В. Введение в теорию случайных процессов. М.: Наука, 1977, 568 с.
2. Севастьянов Б.А. Ветвящиеся процессы. М.: Наука, 1971, 436 c.
3. Баруча-Рид А.Т. Элементы теории марковских процессов и их приложения. М.: Наука, 1969, 512 с.
4. Севастьянов Б.А., Калинкин А.В. Ветвящиеся случайные процессы с взаимодействием частиц. - Доклады АН СССР, 1982, т. 264, вып. 2, с. 306-308.
5. Калинкин А.В. Случайные процессы в естествознании: дискретное фазовое пространство. М.: МГТУ им. Н.Э.Баумана, 1999, 40 с.
6. Калинкин А.В. Марковские ветвящиеся процессы с взаимодействием. - Усп. матем. наук, 2002, т. 57, вып. 2, с. 23-84.

• О работах советских математиков по основаниям физической статистики 30-40-х гг. Обозрение прикладной и промышленной математики. Серия "Вероятность и статистика", 1999, т. 6, вып. 1, с. 148-150. (Шестая Всероссийская школа-коллоквиум по стохастическим методам. Тезисы докладов. Самара, 15 - 21 августа 1999 г.)

В докладе рассматривается следующая схема литературных ссылок:

Указанные работы посвящены одной из фундаментальных проблем современного естествознания, - проблеме построения макроскопических моделей вещества на основе молекулярно-кинетических представлений. Статистический метод основан на микроскопических представлениях и основная задача формулируется следующим образом: зная законы поведения частиц, из которых построена система (молекулы, атомы и т. п.), установить законы поведения макроскопического количества вещества, в первую очередь, феноменологические законы, которые устанавливают связь между непосредственно наблюдаемыми величинами (объем, концентрация реагентов и т. д.) [2].

В неравновесной физической статистике при рассмотрении систем взаимодействующих частиц используются i-частичные функции распределения F_i(t; x₁, x₂, ... , x_i), которые описывают расположение i частиц одного типа на фазовом пространстве (-¥, ¥) в момент времени t, t Î [0, ¥). В работе [3] получена цепочка уравнений для таких функций распределения. Считается, что одночастичная функция распределения F₁(t; x₁) удовлетворяет кинетическому уравнению, которое имеет вид

(1)

где A(x₁,F₁) - некоторый функционал. При известной функции F₁(t; x₁) вид i-частичных функций распределения находят с помощью цепочки уравнений.

Функция распределения F_i(t; x₁, x₂, ... , x_i) является симметричной относительно переменных x₁, x₂, ... , x_i [3], т. к. все микрочастицы одного типа неразличимы. Теорема де Финетти-Хинчина [6] утверждает, что свойство симметричной зависимости для бесконечной последовательности случайных величин эквивалентно свойству условной независимости и условной одинаковой распределенности. Применительно к i-частичным функциям распределения получаем

F_i(t; x₁, x₂, ... , x_i) = ò_-¥^¥ j(x₁|y) j(x₂|y) ... j(x_i|y) dH(t,y),     i = 1,2,...,       (2)

и задача вывода кинетического уравнения сводится к поиску осредняющей меры H(t,y) и выводу уравнения для одночастичной условной функции распределения j(x|y) [9], [10], [11].

Для применения теоремы о симметрии к системам взаимодействующих частиц математическое определение такой системы должно быть строгим с точки зрения теории вероятностей - определено вероятностное пространство (W, A, P). Ряд известных кинетических уравнений не являются строго определенными [2]. В теории случайных процессов исследуются два кинетических уравнения: уравнение диффузионного процесса [1], и уравнение ветвящегося процесса [4], [7]. Случаи диффузионного и ветвящегося процессов соответствуют вырождению формулы (2), когда осредняющая мера сосредоточена в единственной точке. Частицы в этих процессах независимы:

Для ветвящегося процесса в [4] получено уравнение вида (1) для одночастичной производящей функции переходных вероятностей. Первая система уравнений Колмогорова для марковских процессов классов [4], [5] является цепочкой уравнений для i-частичных функций распределения [9], [11].

В рассматриваемых работах использованы условия независимости: марковское свойство; корреляция между положениями микрочастиц ослабевает по мере увеличения расстояния между ними; независимое протекание акта столкновения атомов, молекул и т. п. в разреженном газе. Последнее условие используется в кинетическом уравнении Больцмана; применительно к марковским процессам со счетным числом состояний это условие введено в [2] для бимолекулярных процессов, и в [5] для ветвящихся процессов с взаимодействием частиц [8].

1. Колмогоров А.Н. Об аналитических методах в теории вероятностей. - Усп. матем. наук, 1938, т. 5, с. 5-41. (Пер. с нем.: Math. Ann., 1931, Bd. 104, S. 415-458.)
2. Леонтович М.А. Основные уравнения кинетической теории газов с точки зрения теории случайных процессов. - Журн. эксперим. и теорет. физики, 1935, т. 5, вып. 3-4, с. 211-231.
3. Боголюбов Н.Н. Проблемы динамической теории в статистической физике. М.-Л.: Гостехиздат, 1946, 120 с.
4. Колмогоров А.Н., Дмитриев Н.А. Ветвящиеся случайные процессы. - Доклады АН СССР, 1947, т. 56, вып. 1, с. 7-10.
5. Севастьянов Б.А. Случайные процессы со столкновениями частиц. М.: 1949, 7 с. ( рукопись).
6. Хинчин А.Я. О классах эквивалентных событий. - Доклады АН СССР, 1952, т. 85, вып. 4, с. 713-714. (Перепечатано: А.Я. Хинчин. Избранные труды по теории вероятностей. М.: Научное издательство ТВП, 1995, с. 358-360.
7. Севастьянов Б.А. Ветвящиеся процессы. М.: Наука, 1971, 436 c.
8. Севастьянов Б.А., Калинкин А.В. Ветвящиеся случайные процессы с взаимодействием частиц. - Доклады АН СССР, 1982, т. 264, вып. 2, с. 306-308.
9. Калинкин А.В. Некоторые вопросы естествознания и развитие теории случайных процессов (1925-1955 гг.). М.: 1983, 150 с. ( рукопись).
10. Калинкин А.В. Третье уравнение Колмогорова для ветвящегося процесса с взаимодействием частиц. - Доклады РАН, 2000, т. 371, вып. 2, с. 159-162.
11. Калинкин А.В. Теорема Финетти-Хинчина о симметрии в неравновесной статистической физике. - Доклады РАН, 2000, т. 370, вып. 4, с. 457-460.

• Естественная структура множества марковских процессов. Обозрение прикладной и промышленной математики. Серия "Вероятность и статистика", 1998, т. 5, вып. 2, с. 222-223. (Пятая Всероссийская школа-коллоквиум по стохастическим методам. Тезисы докладов. Йошкар-Ола, 6 - 12 декабря 1998 г.)

Структура множества M марковских процессов со счетным числом состояний Nⁿ, N = {0,1,2,...}, и непрерывным временем t Î [0, ¥), определяется приложениями теории марковских процессов в неравновесной статистической физике и формальной химической кинетике:

(1)

где B₁ - класс маpковских ветвящихся процессов [4, гл. 4], B₂ - класс ветвящихся процессов с взаимодействием частиц [5, 6], классы B₃, и множество M₁ - определены в [10] указанием инфинитезимальных характеристик. Структура (1) основана на интерпретации точки фазового пространства a = (a₁, a₂, ... , a_n) Î Nⁿ как такого состояния некоторой физической системы, в котором имеется совокупность частиц S_a состоящая из a₁ частиц типа T₁, a₂ частиц типа T₂, ... , a_n частиц типа T_n; переход случайного процесса в другое состояние, - результат взаимодействия одного из комплексов частиц S_e, e Î A, где A Ì Nⁿ - заданное конечное множество [5].

Множество M₁ выделяется из множества M условием независимости, известным из кинетического уравнения Больцмана [2]: результат взаимодействия комплекса частиц S_e не зависит от наличия других частиц. Первая (обратная) система дифференциальных уравнений Колмогорова для переходных вероятностей P_ab(t), a,b Î Nⁿ является цепочкой уравнений [3] для a-частичных функций распределения F_a(t) = {P_ab(t), b Î Nⁿ}. a-частичные функции распределения обладают свойствами симметрии [3], в соответствии с принципом тождественности частиц [1]. Множество M₁ в некотором смысле плотно в множестве M [10].

Выбор инфинитезимальных характеристик для специальных классов марковских процессов B₁, B₂, B₃, B₄ связан с соответствующими законами формальной кинетики. Процессы класса B₁ описывают экспоненциальный рост числа "активных" частиц на начальной стадии цепной химической реакции [4]; процессы класса B₃ соответствуют степенному ("медленному") росту числа "активных" частиц в реакции такого же типа [7]. В [2] указано на связь между моделью бимолекулярной химической реакции в виде случайного процесса из класса B₂ и макроскопическим описанием кинетики такой реакции - законом действующих масс. Класс B₄ соответствует обобщениям закона действующих масс, принятым в формальной кинетике.

Для некоторых процессов из классов B₁, B₂ стационарное распределение при совпадает с принятыми в равновесной статистической физике каноническими распределениями [2, 8].

Структура (1) pассматpивается с целью пеpенести, в обобщенном виде, свойство ветвления переходных вероятностей P_ab(t), имеющее место для процессов из класса B₁ [4, с. 117], на классы B₂, B₃, B₄ и множество M₁. Примеры свойства ветвления даны в [9] для процесса из класса B₂ и в [11] для процесса из множества M₁. Свойство ветвления реализует теорему Финетти-Хинчина о рандомизации последовательности симметричных -частичных функций распределения. Свойство ветвления определяет возможность применения математического аппарата производящих функций при рассмотрении марковских случайных процессов с взаимодействием частиц [4, с. 8-9].

В работе [5] была определена структура M É B₂ É B₁.

1. Тождественности принцип. Тождественные частицы. - БСЭ. Изд. 3-е. М.: Советская энциклопедия, 1977, т. 26, с. 30-31.
2. Леонтович М.А. Основные уравнения кинетической теории газов с точки зрения теории случайных процессов. - ЖЭТФ, 1935, т. 5, вып. 3, с. 211-230.
3. Боголюбов Н.Н. Проблемы динамической теории в статистической физике. М.-Л.: Гостехиздат, 1946, 120 с.
4. Севастьянов Б.А. Ветвящиеся процессы. М.: Наука, 1971, 436 с.
5. Севастьянов Б.А. О некоторых типах марковских процессов. - УМН, 1949, т. 4, вып. 4, с. 194.
6. Севастьянов Б.А., Калинкин А.В. Ветвящиеся случайные процессы с взаимодействием частиц. - Доклады АН СССР, 1982, т. 264, вып. 2, с. 306-308.
7. Waugh W.A.O. Uses of the sojourn time series for markovian birth process. - Proceeding of the Sixth Berkeley Sumposium on Mathematical Statistics and Probability. Los Angeles: 1972, v. 3, p. 501-514.
8. Калинкин А.В. Стационарное распределение системы взаимодействующих частиц с дискретными состояниями. - Доклады АН СССР, 1983, т. 268, вып. 6, с. 1362-1364.
9. Калинкин А.В. Свойство ветвления для процесса чистой гибели. - В сб.: Третья Всероссийская школа-коллоквиум по стохастическим методам: Тезисы докладов. (Туапсе, 17 - 24 сентября 1996 г.) М.: ТВП, 1996, с. 62-63.
10. Калинкин А.В. Структура множества марковских процессов. - Вестник РУДН, серия "Прикладная математика и информатика", 1998, вып. 1, с. 93-103.
11. Калинкин А.В. Свойство ветвления для процесса гибели пуассоновского типа. - Теория вероятн. и ее примен., 1999, т. 44, вып. 1, с. 177-178.

• Ветвящийся процесс со схемой взаимодействий частиц вида "хищник-жертва". Обозрение прикладной и промышленной математики. Серия "Вероятность и статистика", 1999, т. 6, вып. 1, с. 137-138. (Шестая Всероссийская школа-коллоквиум по стохастическим методам. Тезисы докладов. Самара, 15 - 21 августа 1999 г.) Совместно с Демидовым С.А, Стрыгиной Л.А.

На множестве состояний N² = {(a₁,a₂), a₁,a₂ = 0,1,...} рассматривается однородный во времени марковский процесс x(t) = (x₁(t), x₂(t)), t Î [0, ¥), с переходными вероятностями

принадлежащий специальному классу процессов со счетным числом состояний [3]: ветвящийся процесс с двумя типами частиц T₁, T₂ и тремя комплексами взаимодействия e¹ = (1,1), e² = (1,0), e³ = (0,1). Возможные взаимодействия представим схемой [4, с. 27]:

Введем производящие функции переходных вероятностей (|s₁| £ 1, |s₂| £ 1)

Вторая (прямая) система дифференциальных уравнений Колмогорова для переходных вероятностей процесса x(t) равносильна линейному уравнению в частных производных второго порядка параболического типа (l ³ 0, m ³ 0, r ³ 0) [3],

(1)

Марковский процесс x(t) является моделью экологической системы "хищник-жертва". Событие {x(t) = (b₁,b₂)} можно интерпретировать как наличие совокупности из b₁ частиц типа T₁ и b₂ частиц типа T₂. Частицы типа T₁ - "хищники", частицы типа T₂ - "жертвы". При данной схеме взаимодействий полагается, что взаимодействие "хищника" и "жертвы" приводит к увеличению числа "хищников". Частицы - "хищники" могут умирать, частицы - "жертвы" могут производить себе подобных. Такое стохастическое описание системы "хищник-жертва" соотносится, при большом числе частиц, с детерминистическим описанием модели "хищник-жертва" в виде нелинейной системы дифференциальных уравнений второго порядка [1]. Приближение системы [1] получают из уравнения (1), переходя к среднему числу частиц A_i(t) = (¶F_(a1,a2) / ¶s_i)|_{s1=1, s2=1}, i = 1,2; полагают начальное состояние равным (na₁, na₂) и n ® ¥.

При r = 0 имеем марковскую модель эпидемии [2].

Для статистического моделирования на ЭВМ случайного процесса x(t) использовано следующее эквивалентное его описание. Пусть процесс находится в начальном состоянии, соответствующем вектору (a₁,a₂). Через случайное время t_(a1,a2)¹, P{t_(a1,a2)¹ < t} = 1 - e^-a₁a₂lt, происходит взаимодействие частицы типа T₁ с частицей типа T₂. Эта пара частиц превращается в новую группу из двух частиц типа T₁; процесс переходит в состояние, соответствующее вектору (a₁ - 1,a₂ + 1). Кроме того, через случайное время t_(a1,a2)², P{t_(a1,a2)² < t} = 1 - e^-a₁mt, происходит гибель частицы типа T₁; процесс переходит в состояние, соответствующее вектору (a₁ - 1,a₂). Через случайное время t_(a1,a2)³, P{t_(a1,a2)³ < t} = 1 - e^-a₂rt, происходит превращение частицы типа T₂ в группу из двух частиц типа T₂; процесс переходит в состояние, соответствующее вектору (a₁,a₂ + 1). Полагается, что случайные величины t_(a1,a2)¹, t_(a1,a2)², t_(a1,a2)³ независимы; в состоянии (a₁,a₂) процесс x(t) находится случайное время t_(a1,a2) = min (t_(a1,a2)¹, t_(a1,a2)², t_(a1,a2)³). Далее аналогичная эволюция случайного процесса.

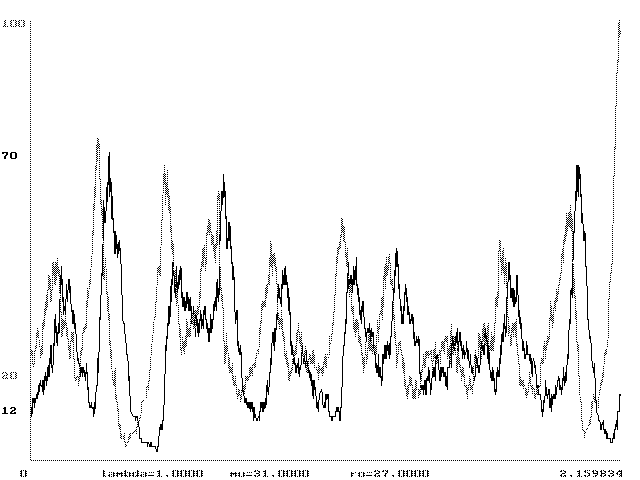
Проведенные статистические эксперименты дают возможность сделать предположение об области K значений параметров m, r (без ограничения общности полагаем l = 1), когда стохастические реализации процесса x(t) устойчиво имеют колебательный вид (характерный для детерминистического описания системы "хищник-жертва"): K = {m > 0, r >0 : c₁ < m/r < c₂}, где c₁, c₂ - некоторые константы. При значении параметров вне области K процесс быстро либо вырождается, либо уходит на бесконечность. На рисунке приведен пример реализации процесса (x₁(t), x₂(t)), t Î [0;2,159834], при начальных условиях x₁(0) = 12, x₂(0) = 20 и значениях параметров l = 1, m = 31, r = 27.

1. Вольтерра В. Математическая теория борьбы за существование. М.: Наука, 1976, 288 с.
2. Эпидемии процесс. В кн.: Математическая энциклопедия. Т. 5. М.: Советская энциклопедия, 1985, с. 1008.
3. Севастьянов Б.А., Калинкин А.В. Ветвящиеся случайные процессы с взаимодействием частиц. - Доклады АН СССР, 1982, т. 264, вып. 2, с. 306-308.
4. Калинкин А.В. Случайные процессы в естествознании: Дискретное фазовое пространство. М.: МГТУ им. Н.Э.Баумана, 1999, 40 с.

• Ветвящийся процесс с взаимодействием частиц. В кн.: Вероятность и математическая статистика: Энциклопедия. М.: Большая Российская энциклопедия, 1999, с. 104.

В е т в я щ и й с я    п р о ц е с с    с    в з а и м о д е й с т в и е м    ч а с т и ц    (branching process with interaction of particles) - модель ветвящегося процесса, в котором новые частицы могут появляться не только при делении частиц, но и в результате взаимодействия некоторых групп частиц. Однородный во времени ветвящийся процесс с взаимодействием частиц является частным случаем марковского процесса с непрерывным временем со счетным множеством состояний. Состояние процесса описывается случайным вектором X(t) = (X₁(t), ..., X_n(t)), k-я компонента которого показывает, что в момент времени t имеется X_k(t) частиц типа T_k. Плотности a_ab = (dP_ab(t)/dt)|_t=0 переходных вероятностей P_ab(t), a,b Î Nⁿ, задаются следующим образом. Дано конечное множество A = {e}, e Î Nⁿ. Пусть за время Dt ¯ 0 любая совокупность частиц, в которую входит по e_k частиц типа T_k, k = 1, ... ,n, e Î A, взаимодействует между собой с вероятностью l_eDt + o(Dt), взаимодействие нескольких таких групп за время Dt возможно с вероятностью o(Dt). Вместо взаимодействующих частиц с вероятностью p_eb появляется группа частиц, соответствующая вектору b, å _b p_eb = 1, p_ee = 0. При этом для a \neq b

a_ab = å _{e Î A} С_a1 ^e₁ ... С_a1 ^e₁ l_e p_e,b-a+e,

a_ab = - å _{e Î A} С_a1 ^e₁ ... С_a1 ^e₁ l_e.

Используя производящие функции [s = (s₁, ... ,s_n), |s_k| £ 1, k = 1, ..., n, s^b = s₁^b₁ ... s_n^b_n, a! = a₁! ... a_n!]

F_a(t; s) = å_b P_ab(t) s^b,

G_b(t; s) = å_a (s^a/a!) P_ab(t),

f_e(s) = l_e (å_b p_eb s^b - s^e),

прямую и обратную системы уравнений Колмогорова для ветвящегося процесса с взаимодействием частиц записывают в виде

Для некоторых моделей ветвящихся процессов с взаимодействием частиц имеют место предельные теоремы для числа финальных частиц, аналогичные теоремам для ветвящихся процессов с независимыми частицами (см. [4], [5]). См. также Эпидемии процесс.

1. Леонтович М.А. Основные уравнения кинетической теории газов с точки зрения теории случайных процессов. - Журн. эксперим. и теорет. физики, 1935, т. 5, вып. 3-4, с. 211-231.
2. Баруча-Рид А.Т. Элементы теории марковских процессов и их приложения, пер. с англ. М.: Наука, 1969, 512 с.
3. Севастьянов Б.А., Калинкин А.В. Ветвящиеся случайные процессы с взаимодействием частиц. - Доклады АН СССР, 1982, т. 264, вып. 2, с. 306-308.
4. Калинкин А.В. Стационарное распределение системы взаимодействующих частиц с дискретными состояниями. Доклады АН СССР, 1983, т. 268, вып. 6, с. 1362-1364.
5. Калинкин А.В. Финальные вероятности для ветвящегося случайного процесса с взаимодействием частиц. Доклады АН СССР, 1983, т. 269, вып. 6, с. 1309-1312.

• Теорема Финетти-Хинчина о симметрии в неравновесной статистической физике. Доклады РАН, 2000, т. 370, вып. 4, с. 457-460. khintchine.ps

РЕФЕРАТ

УДК 531.19:519.21 МАТЕМАТИЧЕСКАЯ ФИЗИКА

В работе анализируются условия, при выполнении которых описание неравновесных состояний физических систем может быть сведено к решению кинетического уравнения для одночастичной функции распределения. Обсуждается применимость принципа тождественности частиц и теоремы Финетти-Хинчина о симметрии к выводу кинетического уравнения. Утверждается, что принцип тождественности частиц является наиболее общим содержательным положением неравновесной физической статистики.

В качестве примера стохастической системы взаимодействующих частиц взята модель бимолекулярной химической реакции T + T ® T в виде марковского случайного процесса при дискретном фазовом пространстве N = {0,1,2,...}. Показано, что обратная система дифференциальных уравнений Колмогорова для марковского процесса гибели и размножения является цепочкой уравнений для n-частичных функций распределения (n Î N). Путем преобразования фазового пространства траекторий частиц процесса с парными взаимодействиями к множеству лесов (возможного для произвольной системы взаимодействующих частиц), получено кинетическое уравнение рассмотренной системы.

• Третье уравнение Колмогорова для ветвящегося процесса с взаимодействием частиц. Доклады РАН, 2000, т. 371, вып. 2, с. 159-162. kolmogorov.ps

РЕФЕРАТ

УДК 519.218.27 МАТЕМАТИКА

Рассмотрен специальный случай однородного во времени марковского процесса со счетным числом состояний N = {0,1,2,...} и непрерывным временем t Î [0, ¥), - ветвящийся процесс с парными взаимодействиями частиц. В частности, для процесса размножения квадратичного типа, когда

P_ii(t) = 1 - i(i - 1)lt + o(t),

P_i,i+1(t) = i(i - 1)lt + o(t),

F_i(t; s) = M jⁱ(X_t, Y_t; s),    i = 0,1,...,

• Метод экспоненциальной производящей функции для случайных блужданий в четверти плоскости. Доклады РАН, 2000, т. 375, вып. 5, с. 583-587. walk.ps

РЕФЕРАТ

УДК 519.21 МАТЕМАТИКА

Для однородного случайного блуждания S_n, n = 0,1,..., на множестве состояний N² = { (a₁, a₂), a₁, a₂ = 0,1,... } получено гиперболическое уравнение в частных производных с постоянными коэффициентами для экспоненциальной производящей функции вероятностей q^{(a₁, a₂)}_(0,g2) остановки блуждания в поглощающей точке границы (0,g₂). В случае переходных вероятностей за один шаг: P{S_n+1 = (a₁ + 1,a₂ - 1) | S_n = (a₁, a₂)} = p₂₀, P{S_n+1 = (a₁ - 1,a₂ - 1) | S_n = (a₁, a₂)} = p₀₀, P{S_n+1 = (a₁ - 1,a₂ + 1) | S_n = (a₁, a₂)} = p₀₂, если a₁ > 0, a₂ >0 (p₂₀ + p₀₂ + p₀₀ = 1); P{S_n+1 = (a₁, a₂) | S_n = (a₁, a₂)} = 1, если a₁ = 0 или a₂ = 0, - прямым решением такого уравнения найдено интегральное представление для q^{(a₁, a₂)}_(0,g2), содержащее эллиптическую функцию Вейерштрасса и функции униформизации римановой поверхности, определяемой характеристическим уравнением p₂₀s₁² + p₀₂s₂² + p₀₀ - s₁s₂ = 0.

В случае неоднородных случайных блужданий на Nⁿ метод приводит к уравнениям в частных производных со степенными коэффициентами и условиями на границах конуса R₊ⁿ.

• Марковские ветвящиеся процессы с взаимодействием. Успехи математических наук, 2002, т. 57, вып. 2, с. 23-84. kalin2u.ps

УДК 519.218.27+531.19

В работе рассматриваются марковские процессы со счетным множеством состояний, интерпретируемые как системы из частиц нескольких типов с взаимодействием комплексами. Результат взаимодействия комплекса частиц не зависит от наличия других частиц в системе. Для нахождения точных замкнутых решений первой и второй систем дифференциальных уравнений Колмогорова для переходных вероятностей используется аппарат многомерных производящих функций. Приведены примеры применения аналитических методов при рассмотрении реальных процессов превращения частиц из различных областей естественных наук.

Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

Г л а в а 1. Cпециальные классы марковских процессов

1.1. Марковские процессы на множестве состояний Nⁿ . . . . . . . . . . . . . . . 27

      1.1.1. Первая и вторая системы дифференциальных уравнений Колмогорова . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

1.2. Многомерные производящие функции . . . . . . . . . . . . . . . . . . . . . . . . . . 29

1.3. Марковские процессы с взаимодействием . . . . . . . . . . . . . . . . . . . . . . . 30

      1.3.1. Интерпретация в виде системы с превращениями частиц . . . . . . 31

      1.3.2. Второе уравнение для производящей функции переходных вероятностей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

1.4. Ветвящиеся процессы с взаимодействием . . . . . . . . . . . . . . . . . . . . . . . . 32

      1.4.1. Первое уравнение для экспоненциальной производящей функции переходных вероятностей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33

      1.4.2. Второе уравнение для производящей функции переходных вероятностей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34

1.5. Ветвящиеся процессы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

1.6. Класс B₃ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

1.7. Структура множества марковских процессов . . . . . . . . . . . . . . . . . . . . 37

Г л а в а 2. Приложения в формальной кинетике

2.1. Типы процессов рождения и гибели . . . . . . . . . . . . . . . . . . . . . . . . . . . 38

      2.1.1. Точные решения уравнений Колмогорова . . . . . . . . . . . . . . . . . 40

      2.1.2. Вероятностные модели цепных реакций . . . . . . . . . . . . . . . . . . . 41

2.2. Марковские модели химических реакций . . . . . . . . . . . . . . . . . . . . . . . 43

      2.2.1. Мономолекулярные реакции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43

      2.2.2. Бимолекулярные реакции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

2.3. Стохастический процесс "хищник-жертва" . . . . . . . . . . . . . . . . . . . . . . 47

Г л а в а 3. Стационарные и финальные вероятности

3.1. Уравнения для предельных вероятностей . . . . . . . . . . . . . . . . . . . . . . . 49

3.2. Стационарное распределение для системы взаимодействующих частиц при дискретных состояниях . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50

3.3. Метод экспоненциальной производящей функции . . . . . . . . . . . . . . . 52

      3.3.1. Популяция с двумя полами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52

      3.3.2. Процесс эпидемии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

      3.3.3. Нерешенные задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58

Г л а в а 4. Третье уравнение Колмогорова

4.1. Нелинейное уравнение теории ветвящихся процессов . . . . . . . . . . . . 60

4.2. Ветвящийся процесс с парными взаимодействиями . . . . . . . . . . . . . . 62

      4.2.1. Решение первого и второго уравнений для процесса гибели квадратичного типа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63

      4.2.2. Третье уравнение для процесса гибели квадратичного типа . . . 66

      4.2.3. Третье уравнение для процесса рождения квадратичного типа 67

4.3. Свойство ветвления и функция Грина для параболических уравнений 69

      4.3.1. Нерешенные задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70

Г л а в а 5. Принцип тождественности частиц и условия независимости

5.1. Цепочка уравнений Боголюбова для марковской системы взаимодействующих частиц . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71

5.2. Теорема Финетти-Хинчина о симметрии и кинетическое уравнение . . . 73

5.3. Преобразование фазового пространства траекторий частиц для системы с взаимодействием к множеству деревьев . . . . . . . . . . . . . . . . . . 75

5.4. Свойство ветвления для процесса простой гибели . . . . . . . . . . . . . . . 77

      5.4.1. Нерешенные задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79

Список литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80

(1) Основным математическим аппаратом современного естествознания остаются дифференциальные уравнения. Условием его применения является рассмотрение детерминированных процессов, или изменения с течением времени макроскопических характеристик физических явлений.

Вероятностные рассмотрения в естествознании возникли во второй половине девятнадцатого века и развивались при микроскопическом подходе к физическим процессам, прежде всего в газах и химических реакциях. Молекулярно-кинетическая теория рассматривает, например, газ как совокупность огромного числа хаотически движущихся частиц (молекулы, атомы и т. д.), взаимодействующих между собой; взаимодействие осуществляется при столкновении частиц или при помощи тех или иных сил. Были выявлены основные требования, накладываемые на вероятностный подход, первоочередная задача формулируется следующим образом: зная законы поведения частиц, из которых построена система, установить, при предельном переходе к большому числу частиц, законы поведения макроскопического количества вещества; в частности, феноменологические законы, которые устанавливают связи между непосредственно наблюдаемыми величинами (давление, объем, концентрация реагентов и т. д.) [102]. Рядом физических экспериментов в первой трети двадцатого века была доказана вероятностная природа микромира, что окончательно привело к пониманию необходимости построения адекватного математического аппарата. "После того, как молекулярные воззрения на строение вещества получили господство в физике, появление в физических теориях новых статистических (или вероятностных) методов исследования стало неизбежным" ([65], с. 7).

Задача построения основания теории случайных процессов решена в 30-40-е годы прошлого столетия работами, в основном, советских математиков. В дальнейшем развитие теории случайных процессов в значительной степени было связано с изучением определенных в этот период теоретико-вероятностных схем.

Применение вероятностных подходов к исследованию природных процессов характеризовалось постепенным переходом от детерминированных механистических представлений к вероятностным представлениям. Первоначально уравнения механики дополняются чуждыми самой механике вероятностными гипотезами (см. анализ кинетического уравнения Больцмана в [79]). Далее успехи в описании физических процессов новыми методами были связаны с отказом от тех или иных детерминистических представлений и вводом вероятностных определений. Полностью свободны от механистических предположений математические схемы теории случайных процессов, чем можно объяснить как универсальную приложимость этих схем в разных областях естествознания, так и глубину развитых для них аналитических методов. В основании теоретико-вероятностных схем лежит понятие вероятностного пространства событий (W, A, P).

Прогресс в понимании природы микромира в последние десятилетия, появление инструментальных средств исследования молекулярного строения вещества, привел к практической необходимости математического описания конкретных микроскопических процессов. Введено значительное число не строго определенных моделей (выполняющих свои функции для узких классов физических явлений), в которых сочетаются элементы детерминированного и вероятностного подходов. Часто эти модели несовместимы с понятием пространства событий; они ограничены в применении аналитических методов. Также исследуются модели на основе классических теоретико-вероятностных схем, в которые включены возникшие в механике понятия, например, при описании взаимодействия потенциал заменяется случайным потенциалом [17], определяются случайные силы и т. д. В таких моделях рассматриваемые для вероятностных схем предельные переходы, в тех или иных случаях, приводят к детерминированным связям. Трудности в приложениях показывают незавершенность теории случайных процессов; в частности, неоднократно отмечалась необходимость введения взаимодействия в теоретико-вероятностных схемах [110].

Развитие теории случайных процессов определяется основополагающими концепциями теории и рассмотрением на этой основе указанных выше фундаментальных проблем (при недостаточности имеющихся на сегодняшний день физических знаний, служащих базой вероятностного подхода в естественных науках). Цель настоящей работы - показать, что возможные шаги в таком направлении могут опираться на теоретико-вероятностные схемы начального периода развития теории случайных процессов и имеющиеся аналитические методы теории.

(2) В работе рассматривается обобщение определенных в работах [79], [104] марковских процессов рождения и гибели со счетным множеством состояний Nⁿ, N = {0,1,2,...}, и непрерывным временем t, t Î [0, ¥). Точка фазового пространства a = (a₁, a₂, ... , a_n) Î Nⁿ интерпретируется как состояние некоторой физической системы, в котором имеется совокупность частиц S_a= a₁T₁ + ... + a_nT_n, состоящая из a₁ частиц типа T₁, ... , a_n частиц типа T_n; переход случайного процесса в другое состояние - результат взаимодействия одного из комплексов частиц S_e, e Î A, где A Ì Nⁿ - заданное множество. Такие процессы моделируют широкий класс реальных систем взаимодействующих частиц в физике, химии, биологии, в которых новые частицы появляются в результате взаимодействия нескольких существующих в данный момент частиц.

Общее определение марковских процессов с взаимодействием при дискретном фазовом пространстве возникает в результате сопоставления ряда работ, связанных последовательностью литературных ссылок [45]:

(0.1)

Взаимосвязи между указанными работами рассматриваются в главе 5 с точки зрения следующего ряда понятий, данных при исследованнии введенных в (0.1) теоретико-вероятностных схем: одночастичные и многочастичные функции распределения; условия независимости; симметрия функций распределения; определение взаимодействия через условия независимости; цепочка уравнений; фазовое пространство траекторий; кинетическое уравнение для одночастичной функции распределения. По мнению автора [49], [50] анализ совокупности данных понятий применительно к марковским процессам приводит к возможности определенного, вытекающего из схемы (0.1), шага в развитии теории случайных процессов. Для подтверждения этого предположения строятся явные решения линейных уравнений Колмогорова для марковских процессов [46], [56].

В статье приведены как известные решения уравнений Колмогорова, так и новые решения. Марковские ветвящиеся процессы с взаимодействием характеризуются применением производящих функций для записи уравнений для переходных вероятностей в виде уравнений в частных производных. Изложенные результаты и постановки задач направлены на вывод замкнутых решений таких уравнений в частных производных. При решении нестационарных и стационарных уравнений Колмогорова получаются выражения для производящих функций искомых вероятностей в виде рядов по специальным функциям; основные аналитические трудности связаны с суммированием этих рядов. Приведение рядов к замкнутой форме дает интегральное представление для производящих функций и при этом подъинтегральные выражения преобразуются к имеющему вероятностную интерпретацию виду. Использовались ортогональные многочлены [46], [47], [61], [62], бесселевы функции [43], [46], гипергеометрические функции [44], [59], [62], эллиптические функции [51], [61].

Отметим, что замкнутые решения уравнений Колмогорова дают возможность простого вывода тех или иных предельных теорем для марковских процессов; примеры таких предельных теорем приведены в статье.

Работа состоит из пяти глав. Каждая глава предваряется кратким описанием ее содержания. Глава 1 содержит вывод основных уравнений, на эту главу опираются все последующие главы. Изложение в каждой из глав 2, 3, 4 не зависит от двух других; выводы главы 5 опираются на результаты главы 4. Главы 2 и 5 являются обзорными, главы 3 и 4 основаны на результатах автора. В работе приведены доказательства теорем, анонсированных в кратких заметках [50], [48], [40], и даны некоторые новые результаты.

Автор благодарен Б.А. Севастьянову за постановку задачи о ветвящихся процессах с взаимодействием, Я.Г. Синаю за предложение о написании статьи, А.М. Зубкову и В.А. Малышеву за ряд замечаний, способствовавших улучшению содержания статьи.

На предшествующую страницу